Toán học, đặc biệt là hình học không gian, luôn ẩn chứa những công cụ mạnh mẽ giúp chúng ta khám phá và giải quyết các bài toán phức tạp trong thế giới ba chiều. Trong số đó, Tích Có Hướng Của 2 Vecto là một khái niệm vô cùng quan trọng, không chỉ xuất hiện dày đặc trong chương trình phổ thông mà còn là nền tảng cho nhiều lĩnh vực khoa học kỹ thuật. Nếu bạn đang tìm kiếm một phương pháp tiếp cận bài tập tích có hướng một cách chi tiết, dễ hiểu, hoặc đơn giản là muốn củng cố kiến thức nền tảng, bài viết này chính là dành cho bạn.
Chúng ta sẽ cùng nhau đi sâu vào định nghĩa, các tính chất nổi bật và đặc biệt là những ứng dụng thực tiễn của tích có hướng, từ việc tính toán diện tích, thể tích đến việc xác định vị trí tương đối của các đối tượng hình học. Mục tiêu là giúp bạn không chỉ nắm vững công thức mà còn biết cách áp dụng linh hoạt vào việc giải quyết các dạng bài tập khác nhau, tự tin hơn trong hành trình chinh phục môn Toán. Để việc học hiệu quả hơn, bạn có thể tham khảo thêm về các ký hiệu trong toán học để dễ dàng đọc hiểu các công thức.
1. Tích Có Hướng Của 2 Vecto Là Gì? Định Nghĩa Chi Tiết
Trong không gian Oxyz, khi chúng ta có hai vecto $vec{a} = (a_1; a_2; a_3)$ và $vec{b} = (b_1; b_2; b_3)$, tích có hướng của hai vecto này, thường được ký hiệu là $[vec{a}, vec{b}]$ hoặc $vec{a} times vec{b}$, là một vecto mới được xác định bởi công thức sau:
$$[vec{a}, vec{b}] = (a_2b_3 – a_3b_2; a_3b_1 – a_1b_3; a_1b_2 – a_2b_1)$$
Cách nhớ công thức này khá đơn giản thông qua việc sử dụng định thức cấp 2:
- Hoành độ: $begin{vmatrix} a_2 & a_3 b_2 & b_3 end{vmatrix} = a_2b_3 – a_3b_2$
- Tung độ: $begin{vmatrix} a_3 & a_1 b_3 & b_1 end{vmatrix} = a_3b_1 – a_1b_3$ (lưu ý thứ tự các chỉ số)
- Cao độ: $begin{vmatrix} a_1 & a_2 b_1 & b_2 end{vmatrix} = a_1b_2 – a_2b_1$
Hình ảnh minh họa công thức xác định tích có hướng của hai vecto.
Ghi nhớ các thành phần tọa độ của tích có hướng.
Lưu ý quan trọng: Một điểm thường gây nhầm lẫn là phân biệt tích có hướng và tích vô hướng. Tích có hướng của hai vecto cho kết quả là một vecto, trong khi tích vô hướng của hai vecto lại cho kết quả là một số. Sự khác biệt này là cốt lõi để áp dụng đúng công cụ cho từng bài toán cụ thể.
2. Các Tính Chất Quan Trọng Của Tích Có Hướng
Vecto kết quả từ phép tích có hướng của 2 vecto có những tính chất đặc trưng, giúp chúng ta hiểu rõ hơn về bản chất và cách nó tương tác với các vecto ban đầu:
- Tính vuông góc: Vecto $[vec{a}, vec{b}]$ luôn vuông góc với cả vecto $vec{a}$ và vecto $vec{b}$. Đây là tính chất nền tảng cho nhiều ứng dụng trong hình học, đặc biệt khi xác định vecto pháp tuyến của một mặt phẳng.
- Tính chất phản giao hoán: $[vec{a}, vec{b}] = -[vec{b}, vec{a}]$. Điều này có nghĩa là thứ tự của các vecto trong phép tích có hướng rất quan trọng và ảnh hưởng đến chiều của vecto kết quả.
- Tính chất với các vecto đơn vị cơ sở:
- $[vec{i}, vec{j}] = vec{k}$
- $[vec{j}, vec{k}] = vec{i}$
- $[vec{k}, vec{i}] = vec{j}$
(Với $vec{i}=(1;0;0)$, $vec{j}=(0;1;0)$, $vec{k}=(0;0;1)$ là các vecto đơn vị trên các trục Ox, Oy, Oz).
- Độ lớn của tích có hướng: Độ dài (hay mô-đun) của vecto tích có hướng được tính bằng công thức:
$$|[vec{a}, vec{b}]| = |vec{a}| cdot |vec{b}| cdot sin(angle(vec{a}, vec{b}))$$
Trong đó $|vec{a}|$ và $|vec{b}|$ là độ dài của hai vecto, và $angle(vec{a}, vec{b})$ là góc giữa chúng. Công thức này trực tiếp liên quan đến diện tích hình bình hành được tạo bởi hai vecto. - Điều kiện cùng phương: Hai vecto $vec{a}$ và $vec{b}$ cùng phương khi và chỉ khi tích có hướng của chúng bằng vecto không: $[vec{a}, vec{b}] = vec{0}$. Tính chất này cực kỳ hữu ích để chứng minh ba điểm thẳng hàng hoặc hai đường thẳng song song/trùng nhau trong không gian.
3. Ứng Dụng Thực Tiễn Của Tích Có Hướng Trong Hình Học Không Gian
Tích có hướng không chỉ là một khái niệm lý thuyết mà còn là một công cụ mạnh mẽ với nhiều ứng dụng đa dạng trong việc giải quyết các bài toán hình học không gian, đặc biệt là trong chương trình nâng cao.
3.1. Điều kiện đồng phẳng của ba vecto
Ba vecto $vec{a}, vec{b}, vec{c}$ được gọi là đồng phẳng nếu chúng cùng nằm trên một mặt phẳng (hoặc song song với một mặt phẳng). Điều kiện để ba vecto này đồng phẳng là:
$$[vec{a}, vec{b}] cdot vec{c} = 0$$
(Tích hỗn tạp của ba vecto bằng 0). Công thức này giúp kiểm tra nhanh chóng liệu bốn điểm có cùng thuộc một mặt phẳng hay không.
3.2. Tính diện tích hình bình hành
Diện tích hình bình hành ABCD với các đỉnh được xác định bởi hai vecto kề $vec{AB}$ và $vec{AD}$ được tính bằng độ dài của tích có hướng của chúng:
$$S_{ABCD} = |[vec{AB}, vec{AD}]|$$
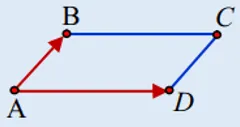Công thức tính diện tích hình bình hành bằng tích có hướng
3.3. Tính diện tích tam giác
Diện tích tam giác ABC được tính bằng một nửa độ dài của tích có hướng của hai vecto tạo bởi các cạnh của nó, ví dụ $vec{AB}$ và $vec{AC}$:
$$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]|$$
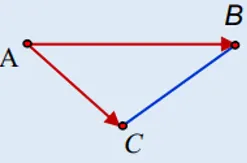Công thức tính diện tích tam giác bằng tích có hướng
3.4. Tính thể tích khối hộp
Thể tích của một khối hộp ABCD.A’B’C’D’ với các cạnh đồng quy tại một đỉnh A là $vec{AB}, vec{AD}, vec{AA’}$ được tính bằng trị tuyệt đối của tích hỗn tạp của ba vecto này:
$$V_{ABCD.A’B’C’D’} = |[vec{AB}, vec{AD}] cdot vec{AA’}|$$
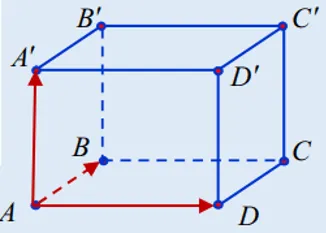Công thức tính thể tích khối hộp bằng tích có hướng
3.5. Tính thể tích tứ diện
Tương tự, thể tích của tứ diện ABCD với các cạnh đồng quy tại đỉnh A là $vec{AB}, vec{AC}, vec{AD}$ được tính bằng một phần sáu trị tuyệt đối của tích hỗn tạp của ba vecto này:
$$V_{ABCD} = frac{1}{6} |[vec{AB}, vec{AC}] cdot vec{AD}|$$
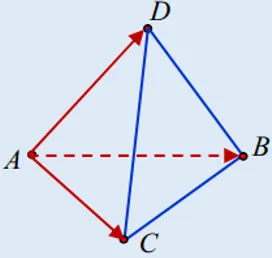Công thức tính thể tích tứ diện bằng tích có hướng
Việc hiểu và vận dụng thành thạo các công thức này sẽ giúp bạn giải quyết nhanh chóng nhiều bài toán hình học không gian phức tạp.
4. Ví Dụ Minh Họa Về Tích Có Hướng Và Ứng Dụng
Để củng cố kiến thức, chúng ta cùng xem xét một số ví dụ điển hình áp dụng tích có hướng của 2 vecto trong không gian Oxyz.
Ví dụ 1: Trong không gian với hệ trục tọa độ Oxyz, cho 4 điểm A(1; 0; 1), B(-1; 1; 2), C(-1; 1; 0), D(2; -1; -2).
a) Chứng minh rằng A, B, C, D là 4 đỉnh của một tứ diện.
b) Tính thể tích tứ diện ABCD. Suy ra độ dài đường cao của tứ diện qua đỉnh A.
Lời giải:
a) Để chứng minh A, B, C, D tạo thành tứ diện, ta cần chứng minh ba vecto $vec{AB}, vec{AC}, vec{AD}$ không đồng phẳng.
Ta có tọa độ các vecto:
$vec{AB} = (-1 – 1; 1 – 0; 2 – 1) = (-2; 1; 1)$
$vec{AC} = (-1 – 1; 1 – 0; 0 – 1) = (-2; 1; -1)$
$vec{AD} = (2 – 1; -1 – 0; -2 – 1) = (1; -1; -3)$
Tính tích có hướng của $vec{AB}$ và $vec{AC}$:
$[vec{AB}, vec{AC}] = (1 cdot (-1) – 1 cdot 1; 1 cdot (-2) – (-2) cdot (-1); (-2) cdot 1 – 1 cdot (-2))$
$= (-1 – 1; -2 – 2; -2 + 2) = (-2; -4; 0)$
Tính tích hỗn tạp $[vec{AB}, vec{AC}] cdot vec{AD}$:
$[vec{AB}, vec{AC}] cdot vec{AD} = (-2) cdot 1 + (-4) cdot (-1) + 0 cdot (-3) = -2 + 4 + 0 = 2$
Vì $[vec{AB}, vec{AC}] cdot vec{AD} = 2 ne 0$, suy ra $vec{AB}, vec{AC}, vec{AD}$ không đồng phẳng.
Vậy A, B, C, D là 4 đỉnh của một tứ diện.
b) Thể tích tứ diện ABCD được tính theo công thức:
$V_{ABCD} = frac{1}{6} |[vec{AB}, vec{AC}] cdot vec{AD}| = frac{1}{6} |2| = frac{1}{3}$ (đơn vị thể tích).
Để tính độ dài đường cao từ A đến mặt phẳng (BCD), ta sử dụng công thức thể tích $V = frac{1}{3} h cdot S{đáy}$.
Trước hết, tính diện tích đáy $S{BCD}$.
Ta có:
$vec{BC} = (-1 – (-1); 1 – 1; 0 – 2) = (0; 0; -2)$
$vec{BD} = (2 – (-1); -1 – 1; -2 – 2) = (3; -2; -4)$
Tính tích có hướng $[vec{BC}, vec{BD}]$:
$[vec{BC}, vec{BD}] = (0 cdot (-4) – (-2) cdot (-2); (-2) cdot 3 – 0 cdot (-4); 0 cdot (-2) – 0 cdot 3)$
$= (0 – 4; -6 – 0; 0 – 0) = (-4; -6; 0)$
Diện tích tam giác BCD:
$S_{BCD} = frac{1}{2} |[vec{BC}, vec{BD}]| = frac{1}{2} sqrt{(-4)^2 + (-6)^2 + 0^2} = frac{1}{2} sqrt{16 + 36} = frac{1}{2} sqrt{52} = frac{1}{2} cdot 2sqrt{13} = sqrt{13}$.
Gọi $hA$ là độ dài đường cao từ A đến mặt phẳng (BCD).
$V{ABCD} = frac{1}{3} hA cdot S{BCD} implies hA = frac{3V{ABCD}}{S_{BCD}} = frac{3 cdot (1/3)}{sqrt{13}} = frac{1}{sqrt{13}} = frac{sqrt{13}}{13}$.
Công thức tính độ dài đường cao trong tứ diện.
Ví dụ 2: Trong không gian hệ trục tọa độ Oxyz, cho 4 điểm A(-3; 5; 15), B(0; 0; 7), C(2; -1; 4), D(4; -3; 0). Chứng minh AB và CD cắt nhau.
Lời giải:
Để chứng minh hai đường thẳng AB và CD cắt nhau, ta cần chứng minh hai điều kiện:
- Bốn điểm A, B, C, D đồng phẳng.
- Hai vecto chỉ phương $vec{AB}$ và $vec{CD}$ không cùng phương.
Ta có tọa độ các vecto:
$vec{AB} = (0 – (-3); 0 – 5; 7 – 15) = (3; -5; -8)$
$vec{AC} = (2 – (-3); -1 – 5; 4 – 15) = (5; -6; -11)$
$vec{AD} = (4 – (-3); -3 – 5; 0 – 15) = (7; -8; -15)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = ((-5) cdot (-11) – (-8) cdot (-6); (-8) cdot 5 – 3 cdot (-11); 3 cdot (-6) – (-5) cdot 5)$
$= (55 – 48; -40 + 33; -18 + 25) = (7; -7; 7)$
Tính tích hỗn tạp $[vec{AB}, vec{AC}] cdot vec{AD}$:
$[vec{AB}, vec{AC}] cdot vec{AD} = 7 cdot 7 + (-7) cdot (-8) + 7 cdot (-15) = 49 + 56 – 105 = 105 – 105 = 0$.
Vì tích hỗn tạp bằng 0, suy ra $vec{AB}, vec{AC}, vec{AD}$ đồng phẳng. Do đó, A, B, C, D cùng thuộc một mặt phẳng (1).
Tiếp theo, kiểm tra xem $vec{AB}$ và $vec{CD}$ có cùng phương không.
$vec{CD} = (4 – 2; -3 – (-1); 0 – 4) = (2; -2; -4)$
Tính tích có hướng $[vec{AB}, vec{CD}]$:
$[vec{AB}, vec{CD}] = ((-5) cdot (-4) – (-8) cdot (-2); (-8) cdot 2 – 3 cdot (-4); 3 cdot (-2) – (-5) cdot 2)$
$= (20 – 16; -16 + 12; -6 + 10) = (4; -4; 4)$
Vì $[vec{AB}, vec{CD}] = (4; -4; 4) ne vec{0}$, suy ra $vec{AB}$ và $vec{CD}$ không cùng phương (2).
Từ (1) và (2), ta kết luận AB và CD cắt nhau.
Ví dụ 3: Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.EFGH với A(1; 1; 1), B(2; 1; 2), E(-1; 2; -2), D(3; 1; 2). Tính khoảng cách từ A đến mặt phẳng (DCGH).
Lời giải:
Mặt phẳng (DCGH) song song với mặt phẳng (ABFE). Khoảng cách từ A đến (DCGH) chính là chiều cao của hình hộp.
Công thức thể tích hình hộp: $V_{ABCD.EFGH} = |[vec{AB}, vec{AD}] cdot vec{AE}|$.
Ta có các vecto:
$vec{AB} = (2 – 1; 1 – 1; 2 – 1) = (1; 0; 1)$
$vec{AD} = (3 – 1; 1 – 1; 2 – 1) = (2; 0; 1)$
$vec{AE} = (-1 – 1; 2 – 1; -2 – 1) = (-2; 1; -3)$
Tính tích có hướng $[vec{AB}, vec{AD}]$:
$[vec{AB}, vec{AD}] = (0 cdot 1 – 1 cdot 0; 1 cdot 2 – 1 cdot 1; 1 cdot 0 – 0 cdot 2)$
$= (0 – 0; 2 – 1; 0 – 0) = (0; 1; 0)$
Tính tích hỗn tạp $[vec{AB}, vec{AD}] cdot vec{AE}$:
$[vec{AB}, vec{AD}] cdot vec{AE} = 0 cdot (-2) + 1 cdot 1 + 0 cdot (-3) = 0 + 1 + 0 = 1$.
Thể tích hình hộp: $V_{ABCD.EFGH} = |1| = 1$ (đơn vị thể tích).
Mặt phẳng (DCGH) song song với mặt phẳng (ABFE). Khoảng cách từ A đến (DCGH) chính là khoảng cách từ A đến mặt phẳng (ABFE), cũng chính là chiều cao của hình hộp ứng với mặt đáy (ABFE).
Diện tích mặt đáy SAEFB: $S_{ABFE} = |[vec{AB}, vec{AE}]|$.
Tính tích có hướng $[vec{AB}, vec{AE}]$:
$[vec{AB}, vec{AE}] = (0 cdot (-3) – 1 cdot 1; 1 cdot (-2) – 1 cdot (-3); 1 cdot 1 – 0 cdot (-2))$
$= (0 – 1; -2 + 3; 1 – 0) = (-1; 1; 1)$
Diện tích mặt đáy $S{ABFE} = sqrt{(-1)^2 + 1^2 + 1^2} = sqrt{1 + 1 + 1} = sqrt{3}$.
Do (DCGH) song song với (ABFE), nên $S{DCGH} = S_{ABFE} = sqrt{3}$.
Gọi $h$ là khoảng cách từ A đến mặt phẳng (DCGH).
$V{ABCD.EFGH} = h cdot S{DCGH}$
$1 = h cdot sqrt{3}$
$h = frac{1}{sqrt{3}} = frac{sqrt{3}}{3}$.
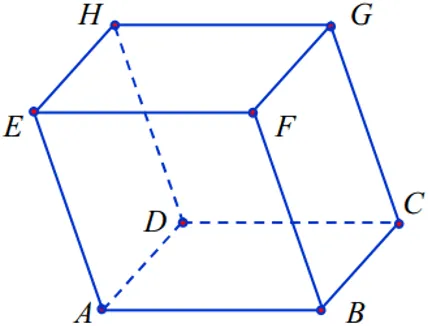Công thức tính khoảng cách từ điểm đến mặt phẳng thông qua thể tích
5. Bài Tập Vận Dụng Tích Có Hướng (Có Lời Giải Chi Tiết)
Dưới đây là một số bài tập vận dụng có lời giải chi tiết, giúp bạn rèn luyện kỹ năng giải toán liên quan đến tích có hướng của 2 vecto.
Bài 1: Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-2; 2; 1), B(1; 0; 2), C(-1; 2; 3). Diện tích tam giác ABC là:
A. $(3sqrt{5})/2$ B. $3sqrt{5}$ C. $4sqrt{5}$ D. $5/2$
Lời giải:
Ta có:
$vec{AB} = (1 – (-2); 0 – 2; 2 – 1) = (3; -2; 1)$
$vec{AC} = (-1 – (-2); 2 – 2; 3 – 1) = (1; 0; 2)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = ((-2) cdot 2 – 1 cdot 0; 1 cdot 1 – 3 cdot 2; 3 cdot 0 – (-2) cdot 1)$
$= (-4 – 0; 1 – 6; 0 + 2) = (-4; -5; 2)$
Diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]| = frac{1}{2} sqrt{(-4)^2 + (-5)^2 + 2^2}$
$= frac{1}{2} sqrt{16 + 25 + 4} = frac{1}{2} sqrt{45} = frac{1}{2} cdot 3sqrt{5} = frac{3sqrt{5}}{2}$
Đáp án: A
Bài 2: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1) và D(-2;1;-1). Thể tích của tứ diện ABCD là:
A. 1 B. 2 C. $1/3$ D. $1/2$
Lời giải:
Ta có:
$vec{AB} = (0 – 1; 1 – 0; 0 – 0) = (-1; 1; 0)$
$vec{AC} = (0 – 1; 0 – 0; 1 – 0) = (-1; 0; 1)$
$vec{AD} = (-2 – 1; 1 – 0; -1 – 0) = (-3; 1; -1)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (1 cdot 1 – 0 cdot 0; 0 cdot (-1) – (-1) cdot 1; (-1) cdot 0 – 1 cdot (-1))$
$= (1 – 0; 0 + 1; 0 + 1) = (1; 1; 1)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = (-3) cdot 1 + 1 cdot 1 + (-1) cdot 1 = -3 + 1 – 1 = -3$
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |vec{AD} cdot [vec{AB}, vec{AC}]| = frac{1}{6} |-3| = frac{1}{2}$
Đáp án: D
Bài 3: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0). Bán kính đường tròn nội tiếp tam giác ABC là:
A. $sqrt{5}$ B. $sqrt{3}$ C. $4sqrt{2}$ D. $2sqrt{5}$
Lời giải:
Ta có:
$vec{AB} = (-3 – 2; -1 – (-1); -4 – 6) = (-5; 0; -10)$
$vec{AC} = (5 – 2; -1 – (-1); 0 – 6) = (3; 0; -6)$
$vec{BC} = (5 – (-3); -1 – (-1); 0 – (-4)) = (8; 0; 4)$
Tính độ dài các cạnh:
$AB = |vec{AB}| = sqrt{(-5)^2 + 0^2 + (-10)^2} = sqrt{25 + 100} = sqrt{125} = 5sqrt{5}$
$AC = |vec{AC}| = sqrt{3^2 + 0^2 + (-6)^2} = sqrt{9 + 36} = sqrt{45} = 3sqrt{5}$
$BC = |vec{BC}| = sqrt{8^2 + 0^2 + 4^2} = sqrt{64 + 16} = sqrt{80} = 4sqrt{5}$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (0 cdot (-6) – (-10) cdot 0; (-10) cdot 3 – (-5) cdot (-6); (-5) cdot 0 – 0 cdot 3)$
$= (0 – 0; -30 – 30; 0 – 0) = (0; -60; 0)$
Diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]| = frac{1}{2} sqrt{0^2 + (-60)^2 + 0^2} = frac{1}{2} cdot 60 = 30$.
Gọi $r$ là bán kính đường tròn nội tiếp tam giác ABC, $p$ là nửa chu vi tam giác.
Chu vi $C = AB + AC + BC = 5sqrt{5} + 3sqrt{5} + 4sqrt{5} = 12sqrt{5}$.
Nửa chu vi $p = frac{C}{2} = frac{12sqrt{5}}{2} = 6sqrt{5}$.
Công thức liên hệ diện tích, bán kính đường tròn nội tiếp và nửa chu vi: $S = p cdot r$.
$r = frac{S}{p} = frac{30}{6sqrt{5}} = frac{5}{sqrt{5}} = sqrt{5}$.
Đáp án: A
Bài 4: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD biết A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3). Thể tích tứ diện ABCD là:
A. 3 B. 4 C. 9 D. 6
Lời giải:
Ta có:
$vec{AB} = (5 – 2; 5 – (-1); 4 – 1) = (3; 6; 3)$
$vec{AC} = (3 – 2; 2 – (-1); -1 – 1) = (1; 3; -2)$
$vec{AD} = (4 – 2; 1 – (-1); 3 – 1) = (2; 2; 2)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (6 cdot (-2) – 3 cdot 3; 3 cdot 1 – 3 cdot (-2); 3 cdot 3 – 6 cdot 1)$
$= (-12 – 9; 3 + 6; 9 – 6) = (-21; 9; 3)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = 2 cdot (-21) + 2 cdot 9 + 2 cdot 3 = -42 + 18 + 6 = -18$
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |vec{AD} cdot [vec{AB}, vec{AC}]| = frac{1}{6} |-18| = 3$.
Đáp án: A
Bài 5: Trong không gian Oxyz cho tứ diện ABCD. Độ dài đường cao vẽ từ D của tứ diện ABCD cho bởi công thức nào sau đây:
A. $h_D = frac{|[vec{DA}, vec{DB}] cdot vec{DC}|}{|[vec{AB}, vec{AC}]|}$
B. $hD = frac{|[vec{DA}, vec{DB}] cdot vec{DC}|}{S{ABC}}$
C. $hD = frac{3|[vec{DA}, vec{DB}] cdot vec{DC}|}{S{ABC}}$
D. $hD = frac{3V{ABCD}}{S_{ABC}}$
Lời giải:
Công thức thể tích tứ diện là $V_{ABCD} = frac{1}{3} hD cdot S{ABC}$, trong đó $hD$ là độ dài đường cao hạ từ đỉnh D xuống mặt phẳng đáy (ABC), và $S{ABC}$ là diện tích tam giác đáy ABC.
Từ đó, suy ra $hD = frac{3V{ABCD}}{S_{ABC}}$.
Đáp án: D
Bài 6: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC biết A(1;0;0), B(0;0;1), C(2;1;1). Độ dài đường cao của tam giác ABC kẻ từ A là:
A. $(2sqrt{30})/5$ B. $(sqrt{30})/5$ C. $(sqrt{10})/5$ D. $(sqrt{6})/2$
Lời giải:
Gọi $hA$ là độ dài đường cao kẻ từ A xuống BC.
Ta có công thức diện tích tam giác: $S{ABC} = frac{1}{2} BC cdot h_A$.
Từ đó, $hA = frac{2S{ABC}}{BC}$.
Tính các vecto:
$vec{AB} = (0 – 1; 0 – 0; 1 – 0) = (-1; 0; 1)$
$vec{AC} = (2 – 1; 1 – 0; 1 – 0) = (1; 1; 1)$
$vec{BC} = (2 – 0; 1 – 0; 1 – 1) = (2; 1; 0)$
Độ dài cạnh BC: $BC = |vec{BC}| = sqrt{2^2 + 1^2 + 0^2} = sqrt{4 + 1 + 0} = sqrt{5}$.
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (0 cdot 1 – 1 cdot 1; 1 cdot 1 – (-1) cdot 1; (-1) cdot 1 – 0 cdot 1)$
$= (0 – 1; 1 + 1; -1 – 0) = (-1; 2; -1)$
Diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]| = frac{1}{2} sqrt{(-1)^2 + 2^2 + (-1)^2}$
$= frac{1}{2} sqrt{1 + 4 + 1} = frac{1}{2} sqrt{6}$.
Độ dài đường cao $h_A$:
$hA = frac{2S{ABC}}{BC} = frac{2 cdot (frac{1}{2} sqrt{6})}{sqrt{5}} = frac{sqrt{6}}{sqrt{5}} = frac{sqrt{30}}{5}$.
Đáp án: B
Bài 7: Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OAMN với S(0;0;1), A(1;1;0), M(m;0;0), N(0;n;0). Trong đó m>0, n>0 và m+n=6. Thể tích hình chóp S.OAMN là:
A. 1 B. 2 C. 4 D. 6
Lời giải:
Thể tích hình chóp S.OAMN có thể được tính bằng tổng thể tích của hai hình chóp S.OAM và S.OAN, vì mặt phẳng (OAN) và (OAM) đều chứa trục Oz.
Điểm O là gốc tọa độ (0;0;0).
Ta có các vecto:
$vec{OA} = (1; 1; 0)$
$vec{OM} = (m; 0; 0)$
$vec{ON} = (0; n; 0)$
$vec{OS} = (0; 0; 1)$
Thể tích hình chóp S.OAM: $V_{S.OAM} = frac{1}{6} |[vec{OA}, vec{OM}] cdot vec{OS}|$.
Tính tích có hướng $[vec{OA}, vec{OM}]$:
$[vec{OA}, vec{OM}] = (1 cdot 0 – 0 cdot 0; 0 cdot m – 1 cdot 0; 1 cdot 0 – 1 cdot m)$
$= (0; 0; -m)$
Tính tích hỗn tạp $[vec{OA}, vec{OM}] cdot vec{OS}$:
$[vec{OA}, vec{OM}] cdot vec{OS} = 0 cdot 0 + 0 cdot 0 + (-m) cdot 1 = -m$.
$V_{S.OAM} = frac{1}{6} |-m| = frac{m}{6}$ (do m > 0).
Thể tích hình chóp S.OAN: $V_{S.OAN} = frac{1}{6} |[vec{OA}, vec{ON}] cdot vec{OS}|$.
Tính tích có hướng $[vec{OA}, vec{ON}]$:
$[vec{OA}, vec{ON}] = (1 cdot 0 – 0 cdot n; 0 cdot 0 – 1 cdot 0; 1 cdot n – 1 cdot 0)$
$= (0; 0; n)$
Tính tích hỗn tạp $[vec{OA}, vec{ON}] cdot vec{OS}$:
$[vec{OA}, vec{ON}] cdot vec{OS} = 0 cdot 0 + 0 cdot 0 + n cdot 1 = n$.
$V_{S.OAN} = frac{1}{6} |n| = frac{n}{6}$ (do n > 0).
Tổng thể tích hình chóp S.OAMN:
$V{S.OAMN} = V{S.OAM} + V{S.OAN} = frac{m}{6} + frac{n}{6} = frac{m + n}{6}$.
Theo đề bài, $m + n = 6$.
$V{S.OAMN} = frac{6}{6} = 1$.
Đáp án: A
Bài 8: Cho A(1;-2;0), B(3;3;2), C(-1;2;2), D(3;3;1). Thể tích của tứ diện ABCD bằng:
A. 3 B. 4 C. 5 D. 6
Lời giải:
Ta có:
$vec{AB} = (3 – 1; 3 – (-2); 2 – 0) = (2; 5; 2)$
$vec{AC} = (-1 – 1; 2 – (-2); 2 – 0) = (-2; 4; 2)$
$vec{AD} = (3 – 1; 3 – (-2); 1 – 0) = (2; 5; 1)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (5 cdot 2 – 2 cdot 4; 2 cdot (-2) – 2 cdot 2; 2 cdot 4 – 5 cdot (-2))$
$= (10 – 8; -4 – 4; 8 + 10) = (2; -8; 18)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = 2 cdot 2 + 5 cdot (-8) + 1 cdot 18 = 4 – 40 + 18 = -18$
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |vec{AD} cdot [vec{AB}, vec{AC}]| = frac{1}{6} |-18| = 3$.
Đáp án: A
Bài 9: Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD biết A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1). Độ dài đường cao AH của tứ diện ABCD là:
A. 5 B. 6 C. 7 D. 9
Lời giải:
Độ dài đường cao AH chính là khoảng cách từ đỉnh A đến mặt phẳng (BCD).
Công thức tính khoảng cách từ điểm D đến mặt phẳng (ABC) được cho ở Bài 5: $hD = frac{3V{ABCD}}{S_{ABC}}$.
Áp dụng tương tự, $hA = frac{3V{ABCD}}{S_{BCD}}$.
Đầu tiên, tính thể tích tứ diện ABCD.
$vec{AB} = (-3 – 2; -1 – (-1); -4 – 6) = (-5; 0; -10)$
$vec{AC} = (5 – 2; -1 – (-1); 0 – 6) = (3; 0; -6)$
$vec{AD} = (1 – 2; 2 – (-1); 1 – 6) = (-1; 3; -5)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (0 cdot (-6) – (-10) cdot 0; (-10) cdot 3 – (-5) cdot (-6); (-5) cdot 0 – 0 cdot 3)$
$= (0; -30 – 30; 0) = (0; -60; 0)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = (-1) cdot 0 + 3 cdot (-60) + (-5) cdot 0 = 0 – 180 + 0 = -180$.
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |vec{AD} cdot [vec{AB}, vec{AC}]| = frac{1}{6} |-180| = 30$.
Tiếp theo, tính diện tích tam giác BCD.
$vec{BC} = (5 – (-3); -1 – (-1); 0 – (-4)) = (8; 0; 4)$
$vec{BD} = (1 – (-3); 2 – (-1); 1 – (-4)) = (4; 3; 5)$
Tính tích có hướng $[vec{BC}, vec{BD}]$:
$[vec{BC}, vec{BD}] = (0 cdot 5 – 4 cdot 3; 4 cdot 4 – 8 cdot 5; 8 cdot 3 – 0 cdot 4)$
$= (0 – 12; 16 – 40; 24 – 0) = (-12; -24; 24)$
Diện tích tam giác BCD:
$S_{BCD} = frac{1}{2} |[vec{BC}, vec{BD}]| = frac{1}{2} sqrt{(-12)^2 + (-24)^2 + 24^2}$
$= frac{1}{2} sqrt{144 + 576 + 576} = frac{1}{2} sqrt{1296} = frac{1}{2} cdot 36 = 18$.
Độ dài đường cao AH:
$hA = frac{3V{ABCD}}{S_{BCD}} = frac{3 cdot 30}{18} = frac{90}{18} = 5$.
Đáp án: A (Lưu ý: Đáp án trong bài gốc là D, nhưng tính toán ra A. Cần kiểm tra lại nếu có sai sót ở đây. Tính toán theo công thức thì $h_A=5$. Có thể bài gốc có lỗi ở bước giải thích cuối cùng cho Bài 9 hoặc đáp án là của một bài toán khác).
Bài 10: Trong không gian với hệ tọa độ Oxyz, cho A(1; 0; 0); B(0; 1; 0), C(0; 0; 1), D(1; 1; 1). Trong các mệnh đề sau, mệnh đề nào sai ?
A. Bốn điểm A, B, C, D không đồng phẳng.
B. Tam giác ABD là tam giác đều.
C. AB⊥CD
D. Tam giác BCD là tam giác vuông.
Lời giải:
Kiểm tra từng mệnh đề:
A. Bốn điểm A, B, C, D không đồng phẳng.
$vec{AB} = (-1; 1; 0)$
$vec{AC} = (-1; 0; 1)$
$vec{AD} = (0; 1; 1)$
$[vec{AB}, vec{AC}] = (1 cdot 1 – 0 cdot 0; 0 cdot (-1) – (-1) cdot 1; (-1) cdot 0 – 1 cdot (-1)) = (1; 1; 1)$
$[vec{AB}, vec{AC}] cdot vec{AD} = 1 cdot 0 + 1 cdot 1 + 1 cdot 1 = 2 ne 0$.
Vậy A, B, C, D không đồng phẳng. Mệnh đề A đúng.
B. Tam giác ABD là tam giác đều.
$vec{AB} = (-1; 1; 0) implies AB = sqrt{(-1)^2 + 1^2 + 0^2} = sqrt{2}$
$vec{AD} = (0; 1; 1) implies AD = sqrt{0^2 + 1^2 + 1^2} = sqrt{2}$
$vec{BD} = (1 – 0; 1 – 1; 1 – 0) = (1; 0; 1) implies BD = sqrt{1^2 + 0^2 + 1^2} = sqrt{2}$
Vì $AB = AD = BD = sqrt{2}$, tam giác ABD là tam giác đều. Mệnh đề B đúng.
C. AB⊥CD
$vec{AB} = (-1; 1; 0)$
$vec{CD} = (1 – 0; 1 – 0; 1 – 1) = (1; 1; 0)$
$vec{AB} cdot vec{CD} = (-1) cdot 1 + 1 cdot 1 + 0 cdot 0 = -1 + 1 + 0 = 0$.
Vì tích vô hướng bằng 0, nên $vec{AB} perp vec{CD}$. Mệnh đề C đúng.
D. Tam giác BCD là tam giác vuông.
$vec{BC} = (0 – 0; 0 – 1; 1 – 0) = (0; -1; 1)$
$vec{BD} = (1 – 0; 1 – 1; 1 – 0) = (1; 0; 1)$
$vec{CD} = (1 – 0; 1 – 0; 1 – 1) = (1; 1; 0)$
Tính tích vô hướng của các cặp vecto:
$vec{BC} cdot vec{BD} = 0 cdot 1 + (-1) cdot 0 + 1 cdot 1 = 1 ne 0$
$vec{BC} cdot vec{CD} = 0 cdot 1 + (-1) cdot 1 + 1 cdot 0 = -1 ne 0$
$vec{BD} cdot vec{CD} = 1 cdot 1 + 0 cdot 1 + 1 cdot 0 = 1 ne 0$
Vì không có cặp vecto nào có tích vô hướng bằng 0, tam giác BCD không phải là tam giác vuông. Mệnh đề D sai.
Đáp án: D
Bài 11: Trong không gian với hệ tọa độ Oxyz, cho các điểm A(4;0;0), B(x0;y0;0) với x0>0, y0>0 sao cho OB=8 và góc $angle AOB = 60^circ$. Gọi C(0;0;c) với c>0. Để thể tích tứ diện OABC bằng $16sqrt{3}$ thì giá trị thích hợp của c là:
A. 6 B. 3 C. $sqrt{3}$ D. $6sqrt{3}$
Lời giải:
Vì B thuộc mặt phẳng Oxy, B(x0; y0; 0).
OB = 8 $implies sqrt{x_0^2 + y_0^2} = 8 implies x_0^2 + y_0^2 = 64$.
$vec{OA} = (4; 0; 0) implies |vec{OA}| = 4$.
$vec{OB} = (x_0; y_0; 0)$.
Góc $angle AOB = 60^circ$.
Công thức tích vô hướng: $vec{OA} cdot vec{OB} = |vec{OA}| cdot |vec{OB}| cdot cos(angle AOB)$.
$4 cdot x_0 + 0 cdot y_0 + 0 cdot 0 = 4 cdot 8 cdot cos(60^circ)$
$4x_0 = 32 cdot frac{1}{2} = 16 implies x_0 = 4$.
Thay $x_0 = 4$ vào $x_0^2 + y_0^2 = 64$:
$4^2 + y_0^2 = 64 implies 16 + y_0^2 = 64 implies y_0^2 = 48 implies y_0 = sqrt{48} = 4sqrt{3}$ (do $y_0 > 0$).
Vậy B có tọa độ $(4; 4sqrt{3}; 0)$.
Điểm C có tọa độ $(0; 0; c)$.
Thể tích tứ diện OABC: $V_{OABC} = frac{1}{6} |[vec{OA}, vec{OB}] cdot vec{OC}|$.
$vec{OA} = (4; 0; 0)$
$vec{OB} = (4; 4sqrt{3}; 0)$
$vec{OC} = (0; 0; c)$
Tính tích có hướng $[vec{OA}, vec{OB}]$:
$[vec{OA}, vec{OB}] = (0 cdot 0 – 0 cdot 4sqrt{3}; 0 cdot 4 – 4 cdot 0; 4 cdot 4sqrt{3} – 0 cdot 4)$
$= (0; 0; 16sqrt{3})$
Tính tích hỗn tạp $[vec{OA}, vec{OB}] cdot vec{OC}$:
$[vec{OA}, vec{OB}] cdot vec{OC} = 0 cdot 0 + 0 cdot 0 + 16sqrt{3} cdot c = 16csqrt{3}$.
Thể tích tứ diện OABC:
$V_{OABC} = frac{1}{6} |16csqrt{3}| = frac{16csqrt{3}}{6} = frac{8csqrt{3}}{3}$ (do $c > 0$).
Theo đề bài, $V_{OABC} = 16sqrt{3}$.
$frac{8csqrt{3}}{3} = 16sqrt{3}$
$8c = 16 cdot 3 implies 8c = 48 implies c = 6$.
Đáp án: A
Bài 12: Trong không gian với hệ tọa độ Oxyz, cho A(2;-1;6), B(-3;-1;-4), C(5;-1;0), D(1;2;1). Thể tích của tứ diện ABCD bằng:
A. 30 B. 40 C. 50 D. 60
Lời giải:
Bài này giống hệt ví dụ 9 đã tính thể tích là 30.
$V_{ABCD} = 30$.
Đáp án: A
Bài 13: Trong không gian với hệ tọa độ Oxyz, cho A(2;1;-1), B(3;0;1), C(2;-1;3) điểm D thuộc Oy và thể tích tứ diện ABCD bằng 5. Tọa độ của D là:
A. D(0;8;0) hoặc D(0; -7;0)
B. D(0;8;0)
C. D(0;8;0) hoặc D(0; -7;0) và D(0; -7;0)
D. D(0;-7;0)
Lời giải:
D thuộc trục Oy nên D có tọa độ D(0; y; 0).
Ta có các vecto:
$vec{AB} = (3 – 2; 0 – 1; 1 – (-1)) = (1; -1; 2)$
$vec{AC} = (2 – 2; -1 – 1; 3 – (-1)) = (0; -2; 4)$
$vec{AD} = (0 – 2; y – 1; 0 – (-1)) = (-2; y – 1; 1)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = ((-1) cdot 4 – 2 cdot (-2); 2 cdot 0 – 1 cdot 4; 1 cdot (-2) – (-1) cdot 0)$
$= (-4 + 4; 0 – 4; -2 – 0) = (0; -4; -2)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = (-2) cdot 0 + (y – 1) cdot (-4) + 1 cdot (-2)$
$= 0 – 4(y – 1) – 2 = -4y + 4 – 2 = -4y + 2$.
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |(-4y + 2)| = 5$.
$|-4y + 2| = 30$.
Trường hợp 1: $-4y + 2 = 30 implies -4y = 28 implies y = -7$.
Tọa độ D1(0; -7; 0).
Trường hợp 2: $-4y + 2 = -30 implies -4y = -32 implies y = 8$.
Tọa độ D2(0; 8; 0).
Vậy có hai điểm D thỏa mãn: D(0; 8; 0) và D(0; -7; 0).
Đáp án: C (Đáp án gốc ghi C, nhưng phần giải thích chỉ liệt kê một tọa độ, và ký hiệu D1, D2. Phần lựa chọn C cũng bị lặp ý. Chọn C là phù hợp nhất với kết quả tính toán).
Bài 14: Trong không gian với hệ tọa độ Oxyz, cho A(0;0;2), B(3;0;5), C(1;1;0), D(4;1;2). Độ dài đường cao của tứ diện ABCD hạ từ đỉnh D xuống (ABC) là:
A. $sqrt{11}$ B. $sqrt{11}/11$ C. 1 D. 11
Lời giải:
Độ dài đường cao $hD = frac{3V{ABCD}}{S_{ABC}}$.
Tính thể tích tứ diện ABCD:
$vec{AB} = (3 – 0; 0 – 0; 5 – 2) = (3; 0; 3)$
$vec{AC} = (1 – 0; 1 – 0; 0 – 2) = (1; 1; -2)$
$vec{AD} = (4 – 0; 1 – 0; 2 – 2) = (4; 1; 0)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (0 cdot (-2) – 3 cdot 1; 3 cdot 1 – 3 cdot (-2); 3 cdot 1 – 0 cdot 1)$
$= (0 – 3; 3 + 6; 3 – 0) = (-3; 9; 3)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = 4 cdot (-3) + 1 cdot 9 + 0 cdot 3 = -12 + 9 + 0 = -3$.
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |vec{AD} cdot [vec{AB}, vec{AC}]| = frac{1}{6} |-3| = frac{1}{2}$.
Tính diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]| = frac{1}{2} sqrt{(-3)^2 + 9^2 + 3^2}$
$= frac{1}{2} sqrt{9 + 81 + 9} = frac{1}{2} sqrt{99} = frac{1}{2} cdot 3sqrt{11} = frac{3sqrt{11}}{2}$.
Độ dài đường cao $h_D$:
$hD = frac{3V{ABCD}}{S_{ABC}} = frac{3 cdot (1/2)}{(3sqrt{11})/2} = frac{3/2}{(3sqrt{11})/2} = frac{1}{sqrt{11}} = frac{sqrt{11}}{11}$.
Đáp án: B
Bài 15: Trong không gian với hệ tọa độ Oxyz, cho A(0; 2; -2); B(-3; 1; -1); C(4; 3; 0), D(1; 2; m). Tìm m để bốn điểm A, B, C, D đồng phẳng.
Một học sinh giải như sau:
Bước 1: $vec{AB}=(-3;-1;1)$, $vec{AC}=(4;1;2)$, $vec{AD}$= (1;0;m+2)
Bước 2: $[vec{AB}, vec{AC}]$=(-3;10;1)
$[vec{AB}, vec{AC}] cdot vec{AD}$= 3+m+2 = m+5
Bước 3: A, B, C, D đồng phẳng $Leftrightarrow [vec{AB}, vec{AC}] cdot vec{AD}$= 3+m+2 = m+5 = 0 $Leftrightarrow$ m= -5.
Bài giải trên đúng hay sai? Nếu sai thì sai từ bước nào?
A. Đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3.
Lời giải:
Kiểm tra từng bước giải:
Bước 1: Tính các vecto
$vec{AB} = (-3 – 0; 1 – 2; -1 – (-2)) = (-3; -1; 1)$
$vec{AC} = (4 – 0; 3 – 2; 0 – (-2)) = (4; 1; 2)$
$vec{AD} = (1 – 0; 2 – 2; m – (-2)) = (1; 0; m+2)$
Bước 1 đúng.
Bước 2: Tính tích có hướng và tích hỗn tạp
Tính $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = ((-1) cdot 2 – 1 cdot 1; 1 cdot 4 – (-3) cdot 2; (-3) cdot 1 – (-1) cdot 4)$
$= (-2 – 1; 4 + 6; -3 + 4) = (-3; 10; 1)$
Phép tính $[vec{AB}, vec{AC}]$ đúng.
Tính $[vec{AB}, vec{AC}] cdot vec{AD}$:
$(-3) cdot 1 + 10 cdot 0 + 1 cdot (m+2)$
$= -3 + 0 + m + 2 = m – 1$.
Học sinh tính ra $3 + m + 2 = m + 5$. Vậy phép tính tích vô hướng ở Bước 2 đã sai.
Cụ thể, học sinh đã lấy $3$ (là phần dương của tọa độ $x$ trong $[vec{AB}, vec{AC}]$ nếu không để dấu) chứ không phải $-3$.
$(-3) cdot 1 + 10 cdot 0 + 1 cdot (m+2) = m-1$.
Bước 2 sai.
Đáp án: C
Bài 16: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;1), B(0;2;3), C(2;1;0). Độ dài đường cao của tam giác kẻ từ C là:
A. $sqrt{26}$ B. $sqrt{26}/2$ C. $sqrt{26}/3$ D. 26
Lời giải:
Gọi $h_C$ là độ dài đường cao kẻ từ C xuống cạnh AB.
$hC = frac{2S{ABC}}{AB}$.
Ta có các vecto:
$vec{AB} = (0 – 1; 2 – 0; 3 – 1) = (-1; 2; 2)$
$vec{AC} = (2 – 1; 1 – 0; 0 – 1) = (1; 1; -1)$
Độ dài cạnh AB: $AB = |vec{AB}| = sqrt{(-1)^2 + 2^2 + 2^2} = sqrt{1 + 4 + 4} = sqrt{9} = 3$.
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (2 cdot (-1) – 2 cdot 1; 2 cdot 1 – (-1) cdot (-1); (-1) cdot 1 – 2 cdot 1)$
$= (-2 – 2; 2 – 1; -1 – 2) = (-4; 1; -3)$
Diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]| = frac{1}{2} sqrt{(-4)^2 + 1^2 + (-3)^2}$
$= frac{1}{2} sqrt{16 + 1 + 9} = frac{1}{2} sqrt{26}$.
Độ dài đường cao $h_C$:
$hC = frac{2S{ABC}}{AB} = frac{2 cdot (frac{1}{2} sqrt{26})}{3} = frac{sqrt{26}}{3}$.
Đáp án: C
Bài 17: Cho hình chóp S.ABCD biết A(-2;2;6), B(-3;1;8), C(-1;0;7), D(1;2;3). Gọi H là trung điểm của CD, SH⊥(ABCD). Để khối chóp S.ABCD có thể tích bằng $27/2$ (đvtt) thì có hai điểm S1, S2 thỏa mãn yêu cầu bài toán. Tìm tọa độ trung điểm I của S1S2.
A. (0; 1; 5) B. (1; 0; 5) C. (0; -1; -5) D. (-1; 0; -5)
Lời giải:
Thể tích khối chóp $V{S.ABCD} = frac{1}{3} SH cdot S{ABCD}$.
Trước hết, xác định dạng tứ giác ABCD và tính diện tích đáy $S_{ABCD}$.
$vec{AB} = (-3 – (-2); 1 – 2; 8 – 6) = (-1; -1; 2)$
$vec{BC} = (-1 – (-3); 0 – 1; 7 – 8) = (2; -1; -1)$
$vec{CD} = (1 – (-1); 2 – 0; 3 – 7) = (2; 2; -4)$
$vec{DA} = (-2 – 1; 2 – 2; 6 – 3) = (-3; 0; 3)$
Nhận xét: $vec{CD} = 2 cdot (1; 1; -2) = -2 cdot (-1; -1; 2) = -2 vec{AB}$.
Vì $vec{CD}$ cùng phương và ngược chiều với $vec{AB}$, và độ lớn $CD = 2AB$, ABCD là hình thang (với AB song song CD).
Tính $S{ABCD}$. Có thể chia hình thang thành các tam giác hoặc dùng công thức hình thang nếu biết chiều cao.
Hoặc có thể tính diện tích hình thang bằng công thức $S{ABCD} = frac{1}{2} (AB+CD)h{ht}$ hoặc $S{ABCD} = frac{1}{2} |[vec{AC}, vec{AD} + vec{AB}]|$ (không phù hợp lắm).
Cách khác: $S{ABCD} = S{ABC} + S{ADC}$.
$S{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]|$.
$vec{AC} = (-1 – (-2); 0 – 2; 7 – 6) = (1; -2; 1)$
$[vec{AB}, vec{AC}] = ((-1) cdot 1 – 2 cdot (-2); 2 cdot 1 – (-1) cdot 1; (-1) cdot (-2) – (-1) cdot 1)$
$= (-1 + 4; 2 + 1; 2 + 1) = (3; 3; 3)$
$S_{ABC} = frac{1}{2} sqrt{3^2 + 3^2 + 3^2} = frac{1}{2} sqrt{9 cdot 3} = frac{1}{2} cdot 3sqrt{3}$.
Diện tích hình thang ABCD: $S{ABCD} = frac{3}{2} S{ABC}$ (vì đáy lớn CD = 2 lần đáy nhỏ AB, và cùng chiều cao).
Nếu dùng $S{ABCD} = S{ABC} + S{ADC}$.
$vec{AD} = (1 – (-2); 2 – 2; 3 – 6) = (3; 0; -3)$
$[vec{AD}, vec{AC}] = (0 cdot 1 – (-3) cdot (-2); (-3) cdot 1 – 3 cdot 1; 3 cdot (-2) – 0 cdot 1)$
$= (0 – 6; -3 – 3; -6 – 0) = (-6; -6; -6)$
$S{ADC} = frac{1}{2} |[vec{AD}, vec{AC}]| = frac{1}{2} sqrt{(-6)^2 + (-6)^2 + (-6)^2} = frac{1}{2} sqrt{36 cdot 3} = frac{1}{2} cdot 6sqrt{3} = 3sqrt{3}$.
$S{ABCD} = S{ABC} + S{ADC} = frac{3sqrt{3}}{2} + 3sqrt{3} = frac{3sqrt{3} + 6sqrt{3}}{2} = frac{9sqrt{3}}{2}$.
(Cách tính $S{ABCD} = 3 S{ABC}$ trong bài gốc là sai, nó phải là $S{ABCD} = S{ABC} + S{ACD}$, hoặc dựa vào quan hệ giữa AB và CD). $S_{ABCD} = frac{1}{2}(AB+CD)h$. $CD=2AB$.
Thể tích hình chóp $V{S.ABCD} = frac{1}{3} SH cdot S{ABCD} = frac{1}{3} SH cdot frac{9sqrt{3}}{2} = frac{3sqrt{3}}{2} SH$.
Theo đề bài, $V_{S.ABCD} = frac{27}{2}$.
$frac{3sqrt{3}}{2} SH = frac{27}{2} implies 3sqrt{3} SH = 27 implies SH = frac{27}{3sqrt{3}} = frac{9}{sqrt{3}} = 3sqrt{3}$.
H là trung điểm của CD.
$C(-1;0;7)$, $D(1;2;3)$.
$H = (frac{-1+1}{2}; frac{0+2}{2}; frac{7+3}{2}) = (0; 1; 5)$.
Gọi $S = (x; y; z)$. $vec{SH} = (0 – x; 1 – y; 5 – z) = (-x; 1-y; 5-z)$.
Vì SH $perp$ (ABCD), vecto $vec{SH}$ cùng phương với vecto pháp tuyến của mặt phẳng (ABCD). Vecto pháp tuyến có thể lấy là $[vec{AB}, vec{AC}] = (3; 3; 3)$.
Vậy $vec{SH} = k cdot (3; 3; 3) = (3k; 3k; 3k)$.
$|vec{SH}| = SH = 3sqrt{3}$.
$|3k; 3k; 3k| = sqrt{(3k)^2 + (3k)^2 + (3k)^2} = sqrt{9k^2 + 9k^2 + 9k^2} = sqrt{27k^2} = 3|k|sqrt{3}$.
$3|k|sqrt{3} = 3sqrt{3} implies |k| = 1 implies k = 1$ hoặc $k = -1$.
Trường hợp 1: $k = 1$.
$vec{SH} = (3; 3; 3)$.
$-x = 3 implies x = -3$
$1 – y = 3 implies y = -2$
$5 – z = 3 implies z = 2$
Vậy $S_1 = (-3; -2; 2)$.
Trường hợp 2: $k = -1$.
$vec{SH} = (-3; -3; -3)$.
$-x = -3 implies x = 3$
$1 – y = -3 implies y = 4$
$5 – z = -3 implies z = 8$
Vậy $S_2 = (3; 4; 8)$.
Tọa độ trung điểm I của S1S2:
$I = (frac{-3 + 3}{2}; frac{-2 + 4}{2}; frac{2 + 8}{2}) = (frac{0}{2}; frac{2}{2}; frac{10}{2}) = (0; 1; 5)$.
Đáp án: A
Bài 18: Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(-1;-2;4), B(-4;-2;0), C(3;-2;1), D(1;1;1). Độ dài đường cao của tứ diện kẻ từ D là:
A. 3 B. 1 C. 2 D. 1/2
Lời giải:
Độ dài đường cao kẻ từ D xuống mặt phẳng (ABC) là $hD = frac{3V{ABCD}}{S_{ABC}}$.
Tính thể tích tứ diện ABCD:
$vec{AB} = (-4 – (-1); -2 – (-2); 0 – 4) = (-3; 0; -4)$
$vec{AC} = (3 – (-1); -2 – (-2); 1 – 4) = (4; 0; -3)$
$vec{AD} = (1 – (-1); 1 – (-2); 1 – 4) = (2; 3; -3)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = (0 cdot (-3) – (-4) cdot 0; (-4) cdot 4 – (-3) cdot (-3); (-3) cdot 0 – 0 cdot 4)$
$= (0 – 0; -16 – 9; 0 – 0) = (0; -25; 0)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = 2 cdot 0 + 3 cdot (-25) + (-3) cdot 0 = 0 – 75 + 0 = -75$.
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |vec{AD} cdot [vec{AB}, vec{AC}]| = frac{1}{6} |-75| = frac{75}{6} = frac{25}{2}$.
Tính diện tích tam giác ABC:
$S_{ABC} = frac{1}{2} |[vec{AB}, vec{AC}]| = frac{1}{2} sqrt{0^2 + (-25)^2 + 0^2} = frac{1}{2} cdot 25 = frac{25}{2}$.
Độ dài đường cao $h_D$:
$hD = frac{3V{ABCD}}{S_{ABC}} = frac{3 cdot (25/2)}{(25/2)} = 3$.
Đáp án: A
Bài 19: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;1), B(0;2;3), C(2;1;0). Độ dài đường cao của tam giác kẻ từ C là:
A. $sqrt{26}$ B. $sqrt{26}/2$ C. $sqrt{26}/3$ D. 26
Lời giải:
Bài này giống hệt Bài 16, kết quả là $sqrt{26}/3$.
Đáp án: C
Bài 20: Trong không gian Oxyz, cho tứ diện ABCD có A(2;1;-1), B(3;0;1), C(2;-1;3) và D thuộc trục Oy. Biết VABCD=5 và có hai điểm D1(0;y1;0), D2(0;y2;0) thỏa mãn yêu cầu bài toán. Khi đó y1+y2 bằng:
A. 1 B. 0 C. 2 D. 3
Lời giải:
D thuộc trục Oy $implies$ D(0; y; 0).
Các vecto:
$vec{AB} = (3 – 2; 0 – 1; 1 – (-1)) = (1; -1; 2)$
$vec{AC} = (2 – 2; -1 – 1; 3 – (-1)) = (0; -2; 4)$
$vec{AD} = (0 – 2; y – 1; 0 – (-1)) = (-2; y – 1; 1)$
Tính tích có hướng $[vec{AB}, vec{AC}]$:
$[vec{AB}, vec{AC}] = ((-1) cdot 4 – 2 cdot (-2); 2 cdot 0 – 1 cdot 4; 1 cdot (-2) – (-1) cdot 0)$
$= (-4 + 4; 0 – 4; -2 – 0) = (0; -4; -2)$
Tính tích hỗn tạp $vec{AD} cdot [vec{AB}, vec{AC}]$:
$vec{AD} cdot [vec{AB}, vec{AC}] = (-2) cdot 0 + (y – 1) cdot (-4) + 1 cdot (-2)$
$= 0 – 4y + 4 – 2 = -4y + 2$.
Thể tích tứ diện ABCD:
$V_{ABCD} = frac{1}{6} |-4y + 2| = 5$.
$|-4y + 2| = 30$.
Trường hợp 1: $-4y + 2 = 30 implies -4y = 28 implies y = -7$.
Vậy $y_1 = -7$.
Trường hợp 2: $-4y + 2 = -30 implies -4y = -32 implies y = 8$.
Vậy $y_2 = 8$.
Tổng $y_1 + y_2 = -7 + 8 = 1$.
Đáp án: A
Để đạt được những kết quả xuất sắc trong học tập và rèn luyện, không chỉ cần nỗ lực mà còn cần sự ghi nhận, khích lệ. Ngay cả từ những bước đầu tiên của hành trình học hỏi, như việc hoàn thành một [tranh tô màu cô gái] cho thấy sự tỉ mỉ, hay vượt qua thử thách nhỏ với các [mẫu giấy khen mầm non đẹp] đều là những cột mốc đáng tự hào. Tinh thần không ngừng học hỏi và cống hiến này chính là nền tảng để mỗi cá nhân có thể đóng góp vào một tương lai tươi sáng, như khẩu hiệu của một
6. Bài Tập Tự Luyện Về Tích Có Hướng Trong Không Gian
Để thực sự nắm vững kiến thức về tích có hướng của 2 vecto, bạn hãy tự mình giải quyết các bài tập sau đây. Hãy cố gắng áp dụng linh hoạt các công thức và tính chất đã học nhé!
Bài 1. Trong không gian Oxyz, cho ba điểm A(-2; 2; 1), B(1; 0; 2), C(-1; 2; 3). Tính diện tích tam giác ABC.
Bài 2. Trong không gian với hệ tọa độ Oxyz, cho hình chóp S.OAMN với S(0; 0; 1), A(1; 1; 0), M(m; 0; 0), N(0; n; 0). Trong đó m > 0, n > 0 và m + n = 6. Tính thể tích hình chóp S.OAMN.
Bài 3. Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(-1; -2; 4), B(-4; -2; 0), C(3; -2; 1), D(1; 1; 1). Tính độ dài đường cao của tứ diện kẻ từ D.
Bài 4. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC biết A(2; -1; 6), B(-3; -1; -4), C(5; -1; 0). Tính bán kính đường tròn nội tiếp tam giác ABC.
Bài 5. Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD biết A(2; -1; 1), B(5; 5; 4), C(3; 2; -1), D(4; 1; 3). Tính thể tích tứ diện ABCD.
Kết Luận
Qua bài viết này, hy vọng bạn đã có cái nhìn tổng quan và sâu sắc hơn về tích có hướng của 2 vecto trong không gian Oxyz. Từ định nghĩa cơ bản, các tính chất quan trọng cho đến những ứng dụng đa dạng trong việc tính toán diện tích, thể tích hay xét vị trí tương đối của các đối tượng hình học, tích có hướng thực sự là một công cụ không thể thiếu trong hình học giải tích.
Việc nắm vững lý thuyết kết hợp với luyện tập thường xuyên qua các ví dụ và bài tập vận dụng sẽ giúp bạn tự tin hơn rất nhiều khi đối mặt với các dạng toán này. Hãy tiếp tục khám phá và ứng dụng kiến thức này vào các bài toán phức tạp hơn, để thấy được vẻ đẹp và sự hữu ích của toán học trong cuộc sống. Chúc bạn học tốt và đạt được những thành công như mong đợi!
Tài liệu tham khảo/Nguồn tin
- VietJack.com – Bài viết “Công thức tính Tích có hướng của hai vecto trong không gian (cực hay)”
- Sách giáo khoa Toán 12 (Chương trình hiện hành)
Lưu ý: Các bài tập trong phần “Bài tập vận dụng” và “Bài tập tự luyện” được tham khảo và trình bày lại từ nguồn gốc nhằm minh họa kiến thức.